Getting Started with ssdtools

Introduction

ssdtools is an R package to fit Species Sensitivity Distributions (SSDs) using Maximum Likelihood and model averaging.

SSDs are cumulative probability distributions that are used to estimate the percent of species that are affected and/or protected by a given concentration of a chemical. The concentration that affects 5% of the species is referred to as the 5% Hazard Concentration (HC₅). This is equivalent to a 95% protection value (PC₉₅). For more information on SSDs the reader is referred to Posthuma, Suter II, and Traas (2001).

In order to use ssdtools you need to install R (see below) or use the Shiny app. The shiny app includes a user guide. This vignette is a user manual for the R package.

Philosophy

ssdtools provides the key functionality required to fit SSDs using Maximum Likelihood and model averaging in R. It is intended to be used in conjunction with tidyverse packages such as readr to input data, tidyr and dplyr to group and manipulate data and ggplot2 (Wickham 2016) to plot data. As such it endeavors to fulfill the tidyverse manifesto.

Installing

In order to install R (R Core Team 2024) the appropriate binary for the users operating system should be downloaded from CRAN and then installed.

Once R is installed, the ssdtools package can be installed (together with the tidyverse) by executing the following code at the R console

install.packages(c("ssdtools", "tidyverse"))

The ssdtools package (and ggplot2 package) can then be loaded into the current session using

library(ssdtools)
library(ggplot2)

Getting Help

To get additional information on a particular function just type ? followed by the name of the function at the R console. For example ?ssd_gof brings up the R documentation for the ssdtools goodness of fit function.

For more information on using R the reader is referred to R for Data Science (Wickham and Grolemund 2016).

If you discover a bug in ssdtools please file an issue with a reprex (repeatable example) at https://github.com/bcgov/ssdtools/issues.

Inputting Data

Once the ssdtools package has been loaded the next task is to input some data. An easy way to do this is to save the concentration data for a single chemical as a column called Conc in a comma separated file (.csv). Each row should be the sensitivity concentration for a separate species. If species and/or group information is available then this can be saved as Species and Group columns. The .csv file can then be read into R using the following

data <- read_csv(file = "path/to/file.csv")

For the purposes of this manual we use the CCME dataset for boron from the ssddata package.

ssddata::ccme_boron
#> # A tibble: 28 × 5
#>    Chemical Species                  Conc Group        Units
#>    <chr>    <chr>                   <dbl> <fct>        <chr>
#>  1 Boron    Oncorhynchus mykiss       2.1 Fish         mg/L 
#>  2 Boron    Ictalurus punctatus       2.4 Fish         mg/L 
#>  3 Boron    Micropterus salmoides     4.1 Fish         mg/L 
#>  4 Boron    Brachydanio rerio        10   Fish         mg/L 
#>  5 Boron    Carassius auratus        15.6 Fish         mg/L 
#>  6 Boron    Pimephales promelas      18.3 Fish         mg/L 
#>  7 Boron    Daphnia magna             6   Invertebrate mg/L 
#>  8 Boron    Opercularia bimarginata  10   Invertebrate mg/L 
#>  9 Boron    Ceriodaphnia dubia       13.4 Invertebrate mg/L 
#> 10 Boron    Entosiphon sulcatum      15   Invertebrate mg/L 
#> # ℹ 18 more rows

Fitting Distributions

The function ssd_fit_dists() inputs a data frame and fits one or more distributions. The user can specify a subset of the following 9 distributions. Please see the distributions and model averaging vignettes for more information regarding appropriate use of distributions and the use of model-averaged SSDs.

ssd_dists_all()
#> [1] "burrIII3"      "gamma"         "gompertz"      "lgumbel"      
#> [5] "llogis"        "llogis_llogis" "lnorm"         "lnorm_lnorm"  
#> [9] "weibull"

using the dists argument.

fits <- ssd_fit_dists(ssddata::ccme_boron, dists = c("llogis", "lnorm", "gamma"))

Coefficients

The estimates for the various terms can be extracted using the tidyverse generic tidy function (or the base R generic coef function).

tidy(fits)
#> # A tibble: 6 × 4
#>   dist   term           est    se
#>   <chr>  <chr>        <dbl> <dbl>
#> 1 llogis locationlog  2.63  0.248
#> 2 llogis scalelog     0.740 0.114
#> 3 lnorm  meanlog      2.56  0.235
#> 4 lnorm  sdlog        1.24  0.166
#> 5 gamma  scale       25.1   7.64 
#> 6 gamma  shape        0.950 0.223

Plots

It is generally more informative to plot the fits using the autoplot generic function (a wrapper on ssd_plot_cdf()). As autoplot returns a ggplot object it can be modified prior to plotting. For more information see the customising plots vignette.

theme_set(theme_bw()) # set plot theme

autoplot(fits) +
  ggtitle("Species Sensitivity Distributions for Boron") +
  scale_colour_ssd()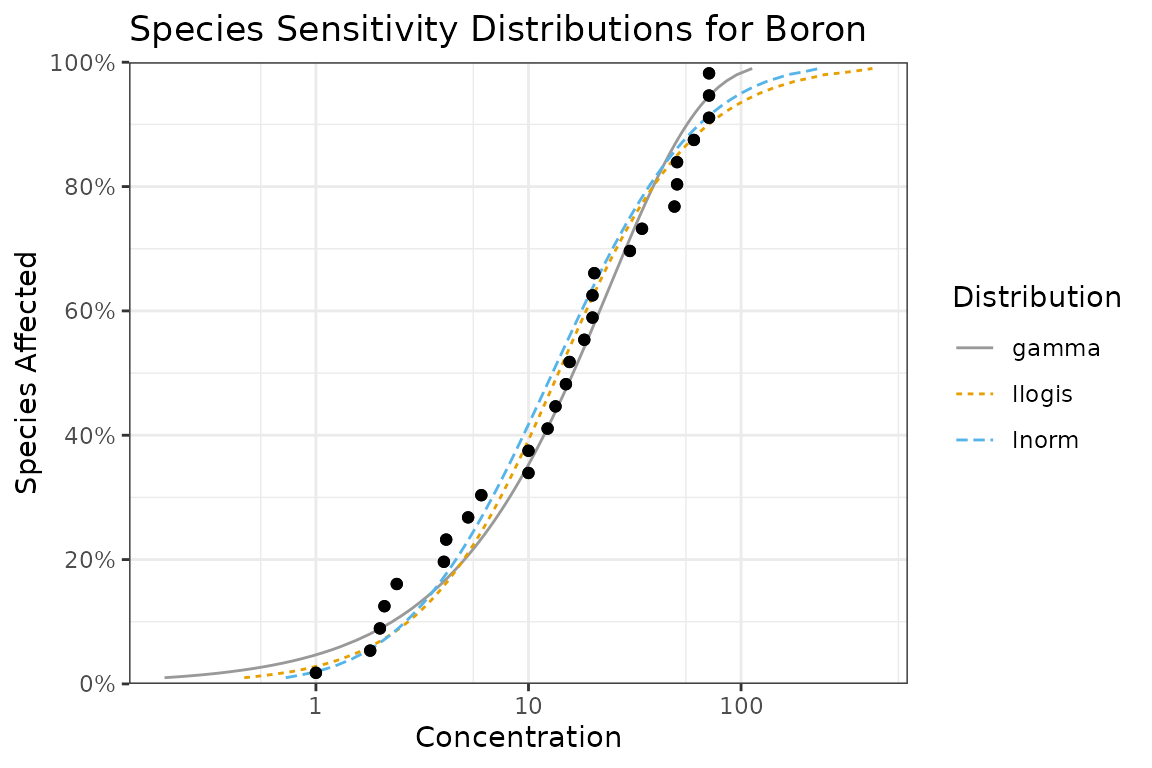

A plot of the CCME boron dataset with the gamma, log-logistic and log-normal distributions with a simple black and white background color scheme.

Selecting One Distribution

Given multiple distributions the user is faced with choosing the “best” distribution (or as discussed below averaging the results weighted by the fit).

ssd_gof(fits)
#> # A tibble: 3 × 9
#>   dist      ad     ks    cvm   aic  aicc   bic delta weight
#>   <chr>  <dbl>  <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
#> 1 llogis 0.487 0.0994 0.0595  241.  241.  244.  3.38  0.11 
#> 2 lnorm  0.507 0.107  0.0703  239.  240.  242.  1.40  0.296
#> 3 gamma  0.440 0.117  0.0554  238.  238.  240.  0     0.595

The ssd_gof() function returns three test statistics that can be used to evaluate the fit of the various distributions to the data.

Anderson-Darling (ad) statistic,
Kolmogorov-Smirnov (ks) statistic and
Cramer-von Mises (cvm) statistic

and three information criteria

Akaike’s Information Criterion (AIC),
Akaike’s Information Criterion corrected for sample size (AICc) and
Bayesian Information Criterion (BIC)

Note if ssd_gof() is called with pvalue = TRUE then the p-values rather than the statistics are returned for the ad, ks and cvm tests.

Following Burnham and Anderson (2002) we recommend the AICc for model selection. The best predictive model is that with the lowest AICc (indicated by the model with a delta value of 0 in the goodness of fit table). In the current example the best predictive model is the gamma distribution but both the lnorm and llogis distributions have some support.

For further information on the advantages of an information theoretic approach in the context of selecting SSDs the reader is referred to Fox et al. (2021).

Averaging Multiple Distributions

Often other distributions will fit the data almost as well as the best distribution as evidenced by delta values < 2 (Burnham and Anderson 2002). In general, the recommended approach is to estimate the average fit based on the relative weights of the distributions (Burnham and Anderson 2002). The AICc based weights are indicated by the weight column in the goodness of fit table. A detailed introduction to model averaging can be found in the Model averaging vignette. A discussion on the recommended set of default distributions can be found in the Distributions vignette.

Estimating the Fit

The predict function can be used to generate model-averaged estimates (or if average = FALSE estimates for each distribution individual) by bootstrapping. Model averaging is based on AICc unless the data censored is which case AICc is undefined. In this situation model averaging is only possible if the distributions have the same number of parameters (so that AIC can be used to compare the models).

set.seed(99)
boron_pred <- predict(fits, ci = TRUE)

The resultant object is a data frame of the estimated concentration (est) with standard error (se) and lower (lcl) and upper (ucl) 95% confidence limits (CLs) by percent of species affected (percent). The object includes the number of bootstraps (nboot) data sets generated as well as the proportion of the data sets that successfully fitted (pboot).

boron_pred
#> # A tibble: 99 × 11
#>    dist    proportion   est    se    lcl   ucl    wt method  nboot pboot samples
#>    <chr>        <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>   <dbl> <dbl> <I<lis>
#>  1 average       0.01 0.267 0.402 0.0419  1.53     1 parame…  1000     1 <dbl>  
#>  2 average       0.02 0.531 0.518 0.110   2.03     1 parame…  1000     1 <dbl>  
#>  3 average       0.03 0.783 0.615 0.198   2.50     1 parame…  1000     1 <dbl>  
#>  4 average       0.04 1.02  0.701 0.300   2.89     1 parame…  1000     1 <dbl>  
#>  5 average       0.05 1.26  0.782 0.407   3.29     1 parame…  1000     1 <dbl>  
#>  6 average       0.06 1.48  0.859 0.520   3.72     1 parame…  1000     1 <dbl>  
#>  7 average       0.07 1.71  0.934 0.645   4.16     1 parame…  1000     1 <dbl>  
#>  8 average       0.08 1.93  1.01  0.769   4.58     1 parame…  1000     1 <dbl>  
#>  9 average       0.09 2.16  1.08  0.896   4.95     1 parame…  1000     1 <dbl>  
#> 10 average       0.1  2.38  1.15  1.03    5.33     1 parame…  1000     1 <dbl>  
#> # ℹ 89 more rows

The data frame of the estimates can then be plotted together with the original data using the ssd_plot() function to summarize an analysis. Once again the returned object is a ggplot object which can be customized prior to plotting.

ssd_plot(ssddata::ccme_boron, boron_pred,
  color = "Group", label = "Species",
  xlab = "Concentration (mg/L)", ribbon = TRUE
) +
  expand_limits(x = 5000) + # to ensure the species labels fit
  ggtitle("Species Sensitivity for Boron") +
  scale_colour_ssd()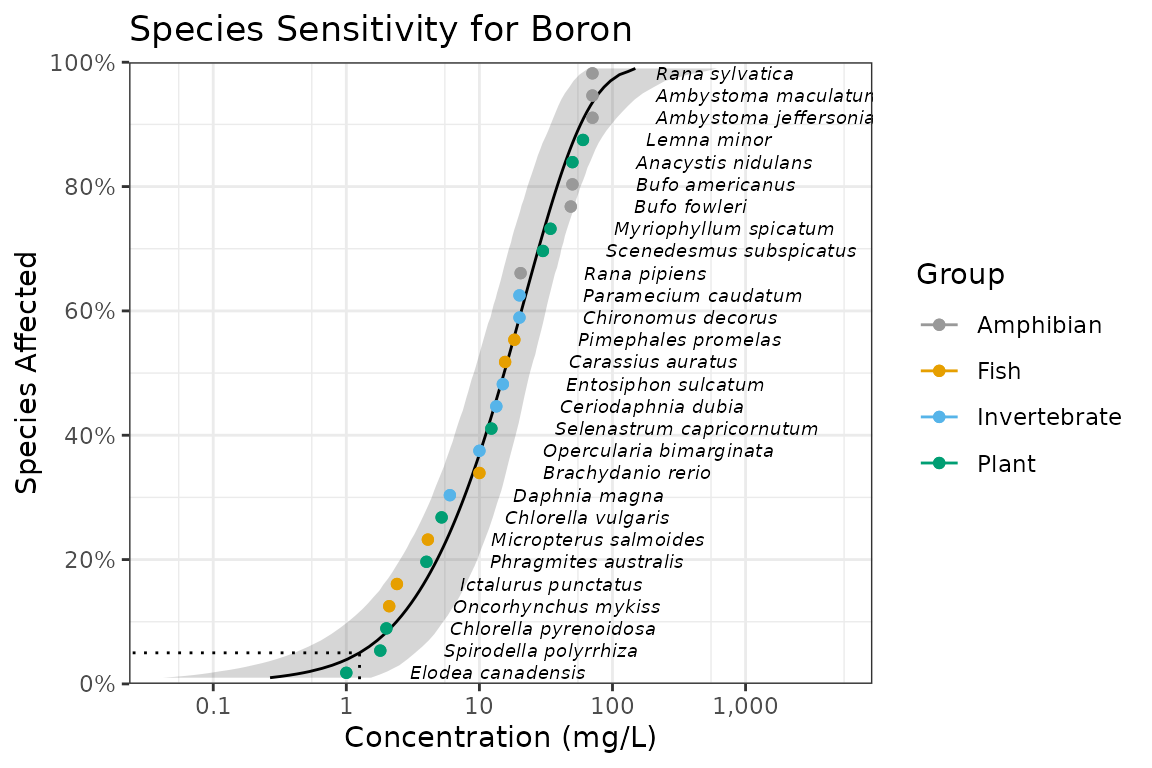

A plot of the CCME boron dataset species colored by group and the model average species sensitivity distribution with a simple black and white background color scheme.

In the above plot the model-averaged 95% confidence interval is indicated by the shaded band and the model-averaged 5%/95% Hazard/Protection Concentration (HC5/ PC₉₅) by the dotted line. Hazard/Protection concentrations are discussed below.

Hazard/Protection Concentrations

The 5% hazard concentration (HC5) is the concentration that affects 5% of the species tested. This is equivalent to the 95% protection concentration which protects 95% of species (PC₉₅). The hazard and protection concentrations are directly interchangeable, and terminology depends simply on user preference.

The hazard/protection concentrations can be obtained using the ssd_hc() function, which can be used to obtain any desired percentage value. The fitted SSD can also be used to determine the percentage of species protected at a given concentration using ssd_hp().

set.seed(99)
boron_hc5 <- ssd_hc(fits, proportion = 0.05, ci = TRUE)
print(boron_hc5)
#> # A tibble: 1 × 11
#>   dist    proportion   est    se   lcl   ucl    wt method    nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>     <dbl> <dbl> <I<lis>
#> 1 average       0.05  1.32 0.849 0.370  3.67     1 parametr…  1000     1 <dbl>
boron_pc <- ssd_hp(fits, conc = boron_hc5$est, ci = TRUE)
print(boron_pc)
#> # A tibble: 1 × 11
#>   dist     conc   est    se   lcl   ucl    wt method     nboot pboot samples  
#>   <chr>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>      <dbl> <dbl> <I<list>>
#> 1 average  1.32     5  3.23 0.586  12.8     1 parametric  1000     1 <dbl [0]>

Censored Data

Censored data is that for which only a lower and/or upper limit is known for a particular species. If the right argument in ssd_fit_dists() is different to the left argument then the data are considered to be censored.

It is important to note that ssdtools doesn’t currently support right censored data.

Let’s produce some left censored data.

boron_censored <- ssddata::ccme_boron |>
  dplyr::mutate(left = Conc, right = Conc)

boron_censored$left[c(3, 6, 8)] <- NA

As the sample size n is undefined for censored data, AICc cannot be calculated. However, if all the models have the same number of parameters, the AIC delta values are identical to those for AICc. For this reason, ssdtools only permits model averaging of censored data for distributions with the same number of parameters. We can call only the default two parameter models using ssd_dists_bcanz(n = 2).

dists <- ssd_fit_dists(boron_censored,
  dists = ssd_dists_bcanz(n = 2),
  left = "left", right = "right"
)

There are less goodness-of-fit statistics available for fits to censored data (currently just AIC and BIC).

ssd_gof(dists)
#> # A tibble: 5 × 9
#>   dist       ad    ks   cvm   aic  aicc   bic delta weight
#>   <chr>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
#> 1 gamma      NA    NA    NA  222.    NA    NA 0      0.376
#> 2 lgumbel    NA    NA    NA  228.    NA    NA 5.67   0.022
#> 3 llogis     NA    NA    NA  226.    NA    NA 3.70   0.059
#> 4 lnorm      NA    NA    NA  224.    NA    NA 1.52   0.176
#> 5 weibull    NA    NA    NA  222.    NA    NA 0.046  0.367

The model-averaged predictions are calculated using AIC

ssd_hc(dists, average = FALSE)
#> # A tibble: 5 × 11
#>   dist    proportion   est    se   lcl   ucl     wt method   nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <chr>    <int> <dbl> <I<lis>
#> 1 gamma         0.05 0.674    NA    NA    NA 0.376  paramet…     0    NA <dbl>  
#> 2 lgumbel       0.05 1.51     NA    NA    NA 0.0221 paramet…     0    NA <dbl>  
#> 3 llogis        0.05 1.15     NA    NA    NA 0.0590 paramet…     0    NA <dbl>  
#> 4 lnorm         0.05 1.32     NA    NA    NA 0.176  paramet…     0    NA <dbl>  
#> 5 weibull       0.05 0.752    NA    NA    NA 0.367  paramet…     0    NA <dbl>
ssd_hc(dists)
#> # A tibble: 1 × 11
#>   dist    proportion   est    se   lcl   ucl    wt method    nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>     <int> <dbl> <I<lis>
#> 1 average       0.05 0.859    NA    NA    NA     1 parametr…     0   NaN <dbl>

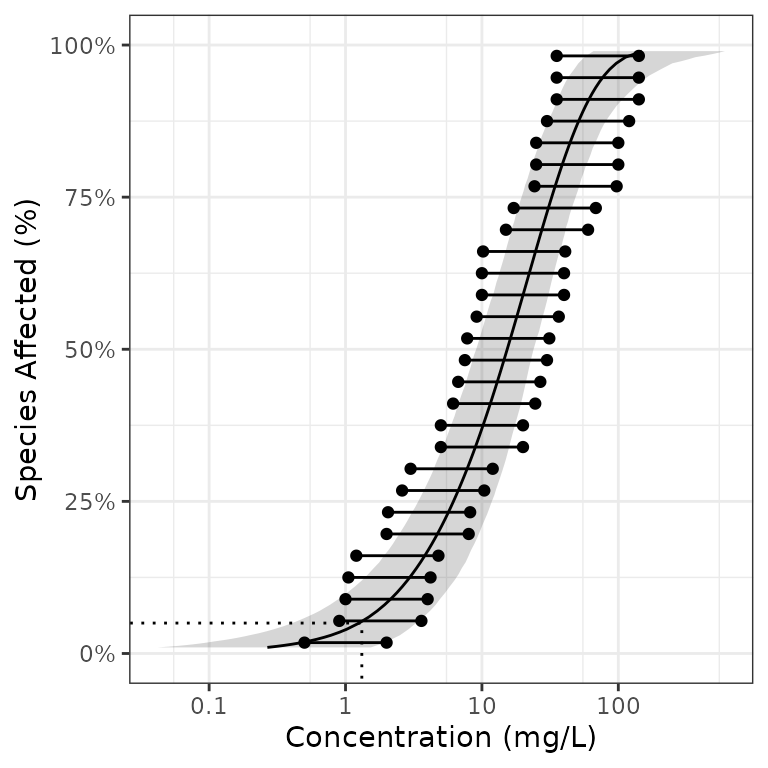
The confidence intervals can currently only be generated for censored data using non-parametric bootstrapping. The horizontal lines in the plot indicate the censoring (range of possible values).

set.seed(99)
pred <- predict(dists, ci = TRUE, parametric = FALSE)

ssd_plot(boron_censored, pred,
  left = "left", right = "right",
  xlab = "Concentration (mg/L)"
)

A plot of the left censored CCME boron dataset with the model average species sensitivity distribution and arrows indicating the censoring.

References

Burnham, Kenneth P., and David R. Anderson, eds. 2002. Model Selection and Multimodel Inference. New York, NY: Springer New York. https://doi.org/10.1007/b97636.

Fox, D. R., R. A. Dam, R. Fisher, G. E. Batley, A. R. Tillmanns, J. Thorley, C. J. Schwarz, D. J. Spry, and K. McTavish. 2021. “Recent Developments in Species Sensitivity Distribution Modeling.” Environmental Toxicology and Chemistry 40 (2): 293–308. https://doi.org/10.1002/etc.4925.

Posthuma, Leo, Glenn W Suter II, and Theo P Traas. 2001. Species Sensitivity Distributions in Ecotoxicology. CRC press. https://www.routledge.com/Species-Sensitivity-Distributions-in-Ecotoxicology/Posthuma-II-Traas/p/book/9781566705783.

R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Wickham, Hadley. 2016. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org.

Wickham, Hadley, and Garrett Grolemund. 2016. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. First edition. Sebastopol, CA: O’Reilly. https://r4ds.had.co.nz.

Licensing

Copyright 2015-2023 Province of British Columbia
Copyright 2021 Environment and Climate Change Canada
Copyright 2023-2024 Australian Government Department of Climate Change, Energy, the Environment and Water

The documentation is released under the CC BY 4.0 License

The code is released under the Apache License 2.0

ssdtools Team

2025-02-20