Confidence Intervals for Hazard Concentrations

ssdtools Team

2024-10-21

Bootstrap confidence intervals

Bootstrapping is a resampling technique used to obtain confidence intervals (CIs) for summary statistics. The team have explored the use of alternative methods for obtaining the CIs of $HC_x$ estimates. This included using the closed-form expression for the variance-covariance matrix of the parameters of the Burr III distribution, coupled with the delta-method, as well as an alternative bootstrap method for the inverse Pareto distribution based on statistical properties of the parameters (D. Fox et al. 2022). In both cases, it appeared that these methods can give results similar to other traditional bootstrapping approaches in much less time, and are therefore potentially worth further investigation. However, implementation of such methods across all the distributions in ssdtools would be a substantial undertaking.

The revised version of ssdtools retains the computationally intensive bootstrapping method to obtain CIs. We recommend a minimum bootstrap sample of 1,000 (the current default - see argument nboot = 1000 in ssd_hc()). However, more reliable results can be obtained using samples of 5,000 or 10,000. We recommend 10,000 bootstrap samples for final reporting.

Parametric versus non-parametric bootstrapping

Burrlioz uses a non-parametric bootstrap method to obtain CIs on the $HC_x$ estimate. Non-parametric bootstrapping is carried out by repeatedly resampling the raw data with replacement, and refitting the distribution many times. The 95% confidence limits (CLs) are then obtained by calculating the lower 0.025th and upper 0.975th quantiles of the resulting $HC_x$ estimates across all the bootstrap samples (typically > 1,000). This type of bootstrap takes into account uncertainty in the distribution fit based on uncertainty in the data.

The ssdtools package by default uses a parametric bootstrap (although non-parametric bootstrapping is also available). Instead of resampling the data, parametric bootstrapping draws a random a set of new data (of the same sample size as the original) from the fitted distribution to repeatedly refit the distribution. Upper and lower 95% bounds are again calculated as the lower 0.025th and upper 0.975th quantiles of the resulting $HC_x$ estimates across all the bootstrap samples (again, typically > 1,000). This approach attempts to capture the uncertainty in the data for a sample size from a given distribution, but it assumes no uncertainty in that original fit.

Using simulation studies the ssdtools team examined bias and compared the resulting coverage of the parametric and non-parametric bootstrapping methods (D. Fox et al. 2022). They found that coverage was better using the parametric bootstrapping method, and this has been retained as the default bootstrapping method in the update to ssdtools although non-parametric bootstrapping is currently the only method available for censored data.

Bootstrapping model-averaged SSDs

Bootstrapping to obtain CIs for individual distributions is relatively straightforward. However, obtaining bootstrap CIs for model-averaged SSDs requires careful consideration, as the procedure is subject to the same problems evident when obtaining model-averaged $HC_x$ estimates (see the Model Averaging SSDs vignette). Model-averaged estimates and/or CIs can be calculated by treating the distributions as constituting a single mixture distribution versus ‘taking the (weighted) mean’. When calculating the model-averaged estimates treating the distributions as constituting a single mixture distribution ensures that ssd_hc() is the inverse of ssd_hp().

Version 2.0 of ssdtools supports three main methods for obtaining bootstrap CIs, and these are discussed in detail below.

Weighted arithmetic mean

Prior to version 2.0, ssdtools calculated the model-averaged estimates and CLs as the weighted (by the AICc values) arithmetic means of the estimates and upper and lower CLs obtained via bootstrapping from each of the candidate distributions independently. This method is not only computationally inefficient but may lead to incorrect results (as described in the Model Averaging SSDs vignette) and has been shown via simulations studies to result in CIs with very low coverage. The current version of ssdtools retains this functionality by setting ci_method = "weighted_arithmetic".

library(ssdtools)

fit <- ssd_fit_dists(data = ssddata::ccme_silver)
set.seed(99)

ssd_hc(fit, ci = TRUE, multi_est = FALSE, ci_method = "weighted_arithmetic")
#> # A tibble: 1 × 11
#>   dist    proportion   est    se    lcl   ucl    wt method   nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>    <dbl> <dbl> <I<lis>
#> 1 average       0.05 0.192 0.216 0.0679 0.861     1 paramet…  1000 0.998 <dbl>

Use of this method is not recommended as it is both technically incorrect and computationally inefficient and only retained to allow users to reproduce previous results.

Weighted mixture distribution

A more theoretically correct way of obtaining model averaged estimates (see the Model Averaging SSDs vignette) and CLs values is to consider the set of distributions as a mixture distribution where the individual distributions are weighted by the AICc values. When we consider the model set as a mixture distribution, bootstrapping is achieved by sampling from the mixture distribution. A method for sampling from mixture distributions has been implemented in ssdtools, via the function ssd_rmulti(), which will generate random samples from a weighted combination of the distributions currently implemented in ssdtools as a mixture distribution.

When bootstrapping from the mixture distribution, a question arises whether the model weights should be re-estimated for every bootstrap sample, or fixed at the values estimated from the models fitted to the original data? This is an interesting question that may warrant further investigation, however our current view is that they should be fixed at their nominal values in the same way that the component distributions to be used in bootstrapping are informed by the fit to the original data. Using simulation studies we explored the coverage and bias of CI values obtained without and without fixing the distribution weights, and results indicate little difference.

The following code can be used to obtain CIs for $HC_x$ estimates via bootstrapping from the weighted mixture distribution (using ssd_rmulti()), with and without fixed weight values respectively.

# Using the multi boostrapping method with fixed weights
ssd_hc(fit, ci = TRUE, ci_method = "multi_fixed")
#> # A tibble: 1 × 11
#>   dist    proportion   est    se    lcl   ucl    wt method   nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>    <dbl> <dbl> <I<lis>
#> 1 average       0.05 0.190 0.207 0.0194 0.824     1 paramet…  1000     1 <dbl>

# Using the multi boostrapping method without fixed weights
ssd_hc(fit, ci = TRUE, ci_method = "multi_free")
#> # A tibble: 1 × 11
#>   dist    proportion   est    se    lcl   ucl    wt method   nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>    <dbl> <dbl> <I<lis>
#> 1 average       0.05 0.190 0.211 0.0223 0.838     1 paramet…  1000     1 <dbl>

Use of this method (without or without fixed weights) is theoretically correct, but is computationally very inefficient.

Weighted bootstrap sample

The developers of ssdtools investigated a third method for obtaining CIs for the model-averaged SSD. This method bootstraps from each of the distributions individually proportional to distributions AICc weight and then combines these into a pooled bootstrap sample before calculating the 95% CLs as the lower 0.025th and upper 0.975th quantiles.

Pseudo-code for this method is as follows:

• For each distribution in the fitdists object, the proportional number of bootstrap samples to draw (nboot_vals) is found using round(nboot * weight), where nboot is the total number of bootstrap samples and weight is the AICc based model weights for each distribution based on the original ssd_fitdist() fit.

• For each of the nboot_vals for each distribution, a random sample of size N is drawn (the total number of original data points included in the original SSD fit) based on the estimated parameters from the original data for that distribution.

• The random sample is re-fit using that distribution.

• $HC_x$ is estimated from the re-fitted bootstrap fit.

• The $HC_x$ estimates for all nboot_vals for all distribution are then pooled across all distributions, and quantile() is used to determine the lower and upper confidence bounds for this pooled weighted bootstrap sample of $HC_x$ values.

This method does not draw random samples from the mixture distribution using ssd_rmulti. While mathematically the method shares some properties with obtaining $HC_x$ estimates via summing the weighted values (weighted arithmetic mean), simulation studies have shown that, as a method for obtaining CIs, this pooled weighted sample method yields similar CIs and coverage to the ssd_rmulti() method but is computationally much faster

This method which is recommended is currently the default method in ssdtools and so can be implemented by simply calling ssd_hc().

# Using a weighted pooled bootstrap sample
ssd_hc(fit, ci = TRUE)
#> # A tibble: 1 × 11
#>   dist    proportion   est    se    lcl   ucl    wt method   nboot pboot samples
#>   <chr>        <dbl> <dbl> <dbl>  <dbl> <dbl> <dbl> <chr>    <dbl> <dbl> <I<lis>
#> 1 average       0.05 0.190 0.214 0.0181 0.816     1 paramet…  1000 0.999 <dbl>

Comparing bootstrapping methods

We have undertaken extensive simulation studies comparing the implemented methods, and the results of these are reported in D. R. Fox et al. (2024). For illustrative purposes, here we compare upper and lower CLs using only a single example data set, the silver data set from the Canadian Council of Ministers of the Environment (CCME) in the ssddata package.

Using the other default settings for ssdtools, we compare the upper and lower CLs for the four bootstrapping methods described above. The upper CLs are relatively similar among the four methods.

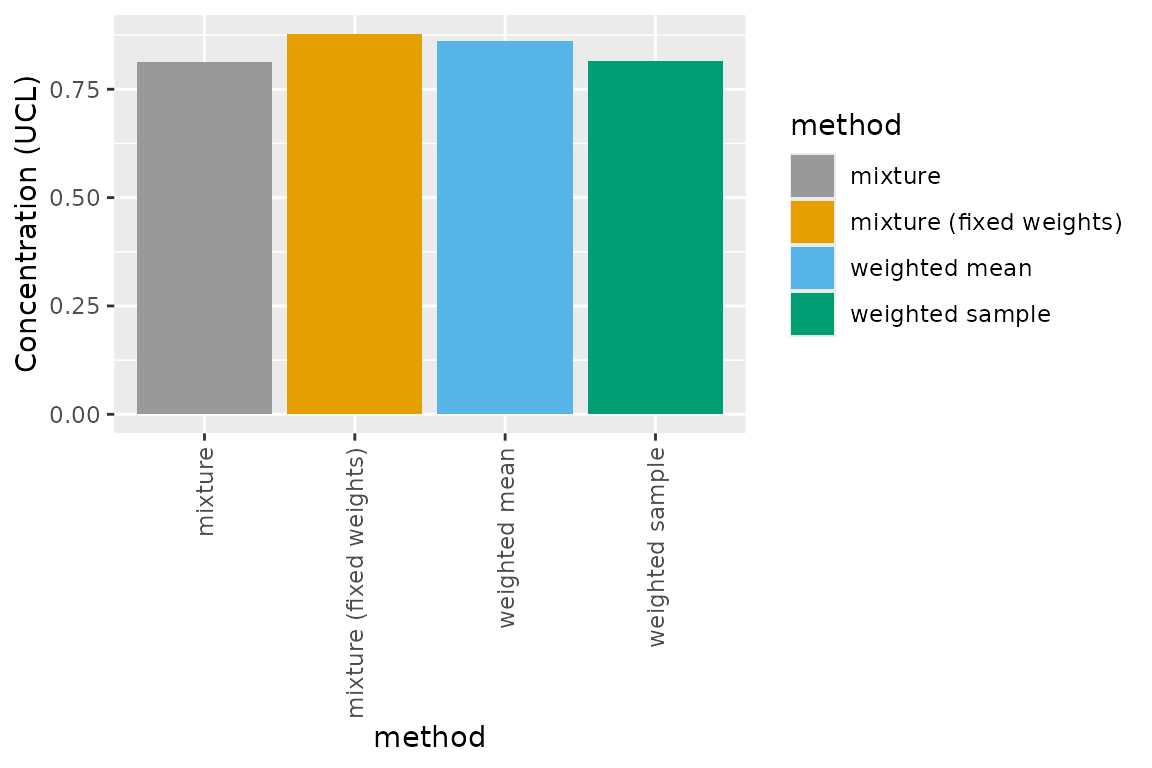
However, the lower CL obtained using the weighted arithmetic mean (the default method implemented in earlier versions of ssdtools) is much higher than the other three methods, potentially accounting for the relatively poor coverage of this method in our simulation studies.

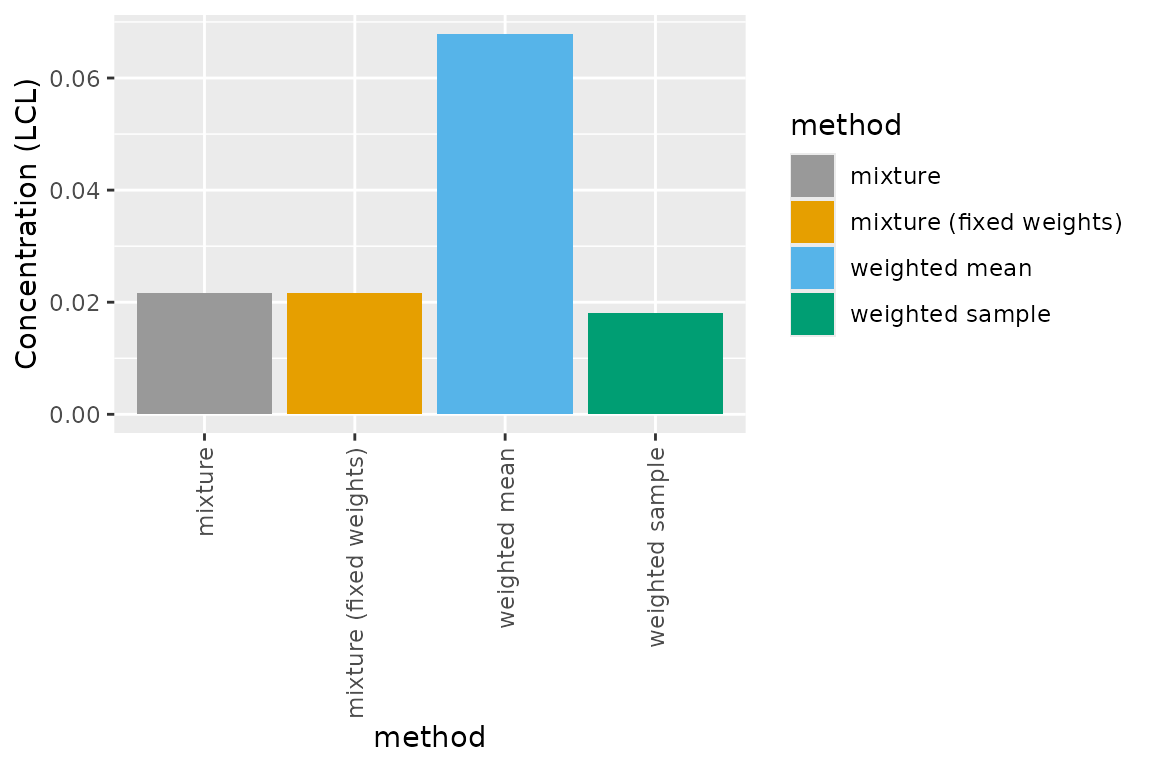
Given the similarity of the upper and lower CLs of the weighted bootstrap sample method compared to the potentially more theoretically correct, but computationally more intensive weighted mixture method (via ssd_rmulti()), we also compared the time taken to undertake bootstrapping across the methods.

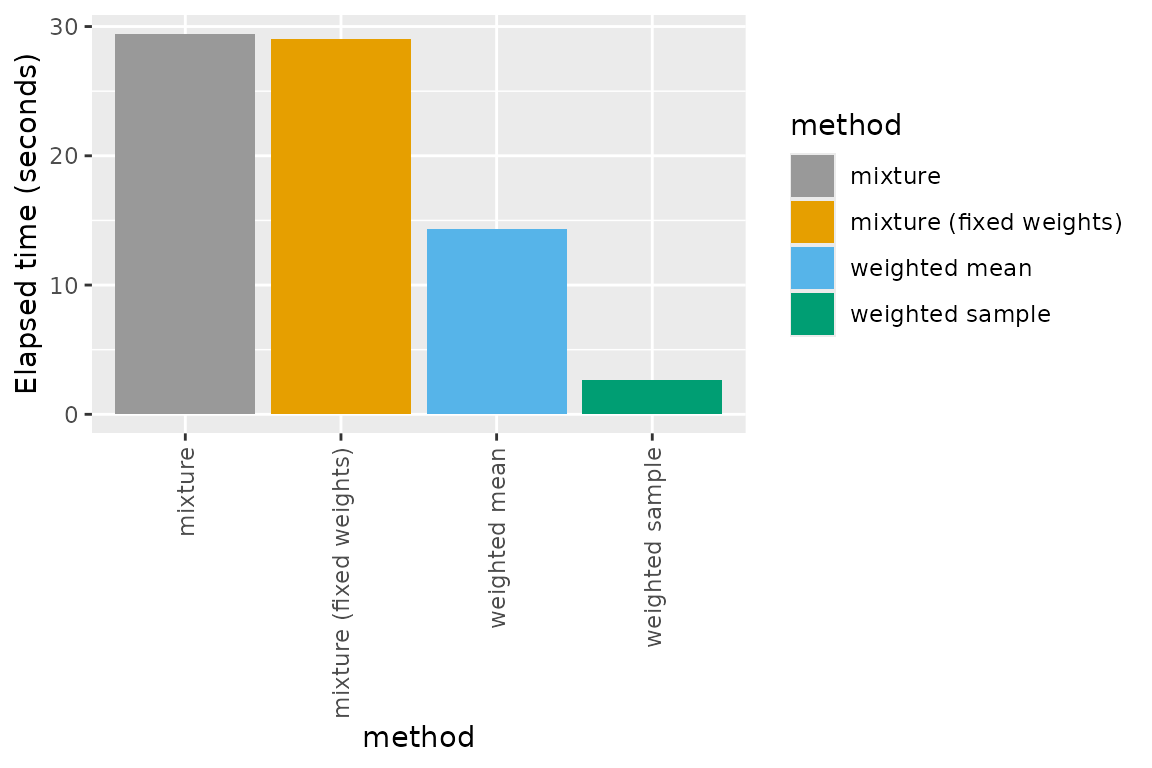
Using the default 1,000 bootstrap samples, the elapsed time to undertake bootstrapping for the mixture method was 29.07 seconds, compared to 2.66 seconds for the weighted bootstrap sample. This means that the weighted bootstrap method is ~ 11 times faster, representing a considerable computational saving across many SSDs. For this reason, this method is currently set as the default method for confidence interval estimation in ssdtools.

References

Fox, David R, Rebecca Fisher, Thorley, and Joseph L. 2024. “Final Report of the Joint Investigation into SSD Modelling and Ssdtools Implementation for the Derivation of Toxicant Guidelines Values in Australia and New Zealand.” Environmetrics Australia; Australian Institute of Marine Science. https://doi.org/10.25845/xtvt-yc51.

Fox, DR, R Fisher, JL Thorley, and C Schwarz. 2022. “Joint Investigation into statistical methodologies Underpinning the derivation of toxicant guideline values in Australia and New Zealand.” Environmetrics Australia; Australian Institute of Marine Science. https://doi.org/10.25845/fm9b-7n28.

Licensing

Copyright 2015-2023 Province of British Columbia
Copyright 2021 Environment and Climate Change Canada
Copyright 2023-2024 Australian Government Department of Climate Change, Energy, the Environment and Water

The documentation is released under the CC BY 4.0 License

The code is released under the Apache License 2.0